Design of Singly reinforced sections – Civil Engineering Projects

Moment of Resistance | Design of Singly reinforced Sections

May 8, 2012 by Designer

Moment of Resistance | Guide to design of Singly reinforced Sections

For the design of Singly reinforced Sections article series, we have covered the following:

Now we will move on with our discussion on “Moment of resistance” and derive the formula for Moment of resistance for balanced section, under-reinforced section and over reinforced section.

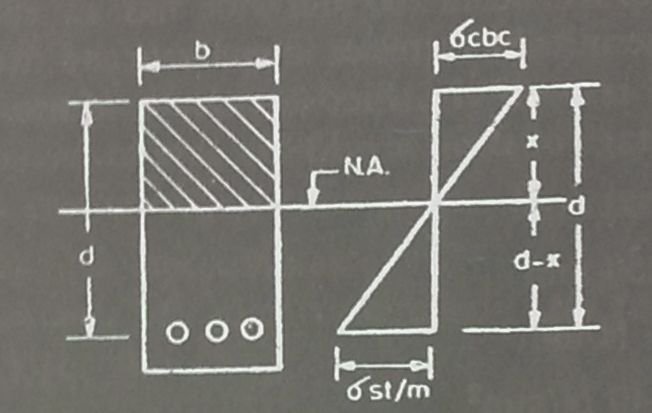
The moment of resistance of the concrete section is the moment of couple formed by the total tensile force (T) in the steel acting at the centre of gravity of reinforcement and the total compressive force (C) in the concrete acting at the centre of gravity (c.g.) of the compressive stress diagram. The moment of resistance is denoted by M.

The distance between the resultant compressive force (C) and tensile force (T) is called the lever arm, and is denoted by z.

Moment of resistance | Singly reinforced Section

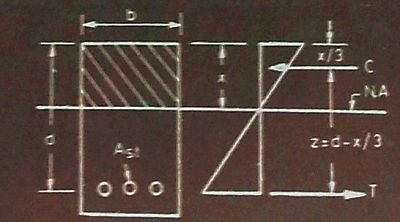
From the diagram above, it is clear that the intensity of compressive stress varies from maximum at the top to zero at the neutral axis.

Therefore, centre of gravity of the compressive force is at a distance x/3 from the top edge of the section.

Therefore, z = d-x/3

Solved Numericals for Singly reinforced Sections | Design Method 2

May 7, 2012 by Designer

Design of Singly reinforced Sections | Method 2

In our article series for Singly reinforced sections, we have covered the following:

Numerical Problem

Find the position of the neutral axis of a reinforced concrete beam 150mm wide and 400mm deep (effective). Area of tensile steel is 804mm2. (modular ratio = m = 18.66)

Step One:

Given that:

b = breadth of a rectangular beam = 150mm

d = effective depth of a beam = 400mm

Ast = cross-sectional area of steel in tension = 804mm2

x = depth of neutral axis below the compression edge

m = modular ratio = 18.66

Taking moments of area of compression and tension sides about neutral axis,

bx.x/2 = mAst (d – x)

Design of Singly reinforced sections | Design Method 2

May 6, 2012 by Designer

Guide to design of Singly reinforced Sections

For “Singly reinforced sections” article series, we have covered the following:

Now we will move on with our discussion on “2nd Design method” for the design of Singly reinforced Sections.

We will follow a simple three-step procedure for the design of singly reinforced sections.

Step One:

Given that:

Dimensions of section (b and d)
Area of tensile steel (Ast)
Modular ratio (m)

From the figure above, we can see that the neutral axis is situated at the centre of gravity of a given section. Therefore, the moments of area on either side are equal.

Design Methods for Singly reinforced Sections

May 4, 2012 by Designer

Singly reinforced sections | Design of RCC structures

Earlier we discussed some basic terms in reference to singly reinforced sections design. It is important that you are thorough with the basic definitions and have complete understanding of stresses in concrete and steel. You should also possess the knowledge of reinforcement and terminology of beams which includes understanding singly reinforced beam, doubly reinforced beam, under reinforced beam, over reinforced beam and balanced reinforced beam.

There are two methods for the design of singly reinforced sections. In this article we will discuss the first method of singly reinforced section in a stepwise manner. The discussion will include the method for determining the value of neutral axis followed by a formula for the area of steel calculations.

Let,

b = breadth of a rectangular beam

d = effective depth of a beam

x = depth of neutral axis below the compression edge

Ast = cross-sectional area of steel in tension

σcbc = permissible compressive stress in concrete in bending

σst = permissible stress in steel

m = modular ratio

Neutral axis

Neutral axis is denoted as NA.

There are two methods for determining the neutral axis depending on the data given.

Stress strain diagram - Singly reinforced section — Stress strain diagram

In this article, we will discuss the first method followed by a couple of numericals for your understanding and then move on to the second method.

Assumptions for Singly reinforced Sections | RCC Structures

May 3, 2012 by Designer

Singly reinforced Sections | Design of RCC Structures

In our series of articles for singly reinforced sections, we have covered the following:

Now, we will move on with our discussion on “assumptions for singly reinforced sections”.

The sections that are plane before bending remain plane after bending, at any cross-section.
All tensile stresses are taken up by steel reinforcement and none by concrete.
The stress to strain relationship of steel and concrete under working load is a straight line.
The modular ratio m has the value 280/3σcbc
There is a perfect adhesion between steel and concrete and no slip takes place between steel and concrete.

Understanding Stresses and Modular ratio | RCC Structures

April 12, 2012 by Designer

Stresses in Steel and Concrete | Building Construction

In one of our previous articles, we discussed “Basic definitions and formulas”.

Now we will move on with our discussion on “Permissible stresses in concrete and steel” and “Understanding Modular ratio”.

Permissible Stresses in Concrete

Reinforced concrete designs make use of M15 grade concrete. The permissible stresses for different grades of concrete is different. They are given below:

Sr. No.	Concrete Grade	M15	M20	M25	M30
1.	Stress in compression Bending	5	7	8.5	10
	Direct	4	5	6	8
2.	Stress in bond (average) for plain bars	0.6	0.8	0.9	1.0
3.	Characteristics compressive strength	15	20	25	30

Also refer for other values in IS:456-1978

Permissible Stresses in Steel

The permissible stresses for different grades of steel are given in the table above.

The different grades steel available in the market with their market names are as follows:

Mild Steel

Grade I steel is known as mild steel. The abbreviation used for Mild steel is (m.s.)

High Tensile deformed steel has two types. They are as follows:

Grade Fe415 (Tor-40 or Tistrong I)
Grade Fe500 (Tor-50 or Tistrong II)

The names of the high tensile deformed steel have been derived from their manufacturers.