What to do on a”Site Inspection/Site Visit”?
Students are always curious and nervous about site visits since this is never taught in any of the colleges in the world. Students have absolutely no idea as to what is to be done when an engineer or Architect is expected to inspect the site. By site, I mean construction site.
Check out his biography: Architect Javed Kachchhi
He is an Architect, Structural Engineer and an Interior Designer. That is the reason why I was so hung up on trying to get in touch with him and write about his experiences about site inspection.
Here we go….
My first question was…
Me: Sir, could you tell us, What exactly is “Site Inspection” or “Site Visit”?
Ar. Javed Kachchhi: Well, let me be very specific. I am sure your readers would like that.
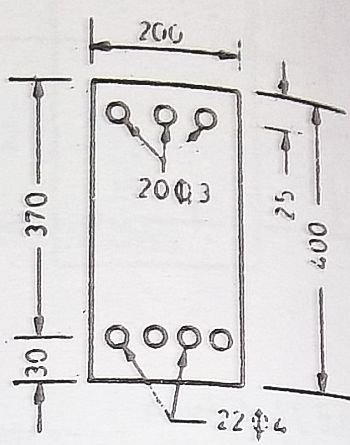
On a site inspection, an Architect/Engineer has to take a complete survey of the site. He has to inspect each and every element that is constructed on site and make sure that the construction is being carried on as per the drawings given by the Architect.
Me: Who monitors the site?
Ar. Javed Kachchhi: Monitoring the site is the work of Site Engineers. Site Engineers have to have a degree in Civil Engineering in order to qualify for the job.