Guide to design of Doubly reinforced Beam
In our article series for “Doubly reinforced sections”, we have covered the following:
What are doubly reinforced sections?
Methods for determining Neutral Axis?
Solved numerical examples for determining Neutral Axis
Numerical examples for practice (Find Neutral axis)
Methods for calculating Moment of Resistance
Numerical example for calculating Moment of resistance
Types of problems in Doubly reinforced sections
Determining stresses in steel and concrete
Numerical example | Stresses in steel and concrete
Now we shall move on with a solved example. This will help you understand the methods in a better way. I suggest that you do them yourselves too. Practice will help you make your concepts more concrete and clear.
Example:
An reinforced concrete beam 200mm x 400mm overall is reinforced with 4 – 22mm⏀ bars with centres 30mm from the bottom edge and 3 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66
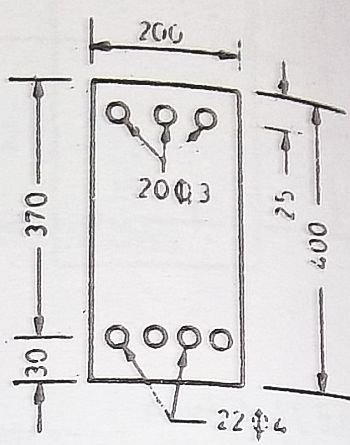
Given that,
Width of the beam = 200mm
Effective depth of the beam = 400 – 30 = 370mm
Distance of compressive steel from the top edge of the beam to the centre of the steel = d’ = 25mm
Modular ratio = m = 18.66
Area of concrete = Asc = 3 x π/4 x (20)2 = 942 mm2
Area of tensile steel = Ast = 4 x π/4 x (22)2 = 1520 mm2
To find x:
Equating moment of area on compression and tension sides about N.A.
bxx/2 + (1.5m – 1)Asc(x – d’) = mAst (d – x)
200x2/2 + (1.5 x 18.66 – 1) 942 (x – 25)
= 18.66 x 1520 (370 – x)
Therefore, x2 + 537.87x – 111299 = 0
Solving the above equation, we get,
x = 159.579mm
Examples for practice
- An reinforced concrete beam 300mm x 600mm overall is reinforced with 6 – 22mm⏀ bars with centres 30mm from the bottom edge and 5 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66
- An reinforced concrete beam 300mm x 600mm overall is reinforced with 4 – 20mm⏀ bars with centres 25mm from the bottom edge and 6 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66
Hi Thanks for the tutition
I have a problem with taking area moments about the nuetral axis
bxx/2 + (1.5m – 1)Asc(x – d’) = mAst (d – x)
I am trying to find guidence on how the area moments were taken.
Only one other source had expanded the line above from
bx2/2-As'(x-d’)+mA’s(x-d’)=mAs(d-x)
where As’ is the area of compression steel
Can you please explain why -As'(x-d’)+mA’s(x-d’) is taken as negative and positive moments please
ANSWERS FOR EXAMPLES :
1)X=188.958mm(approx 189mm)
2)X=151.934mm(approx 152mm)
As'(x-d’) has been taken as negative because it is deduction for the moment of area of steel included in the expression for moment of area of concrete b*x*x/2.Actually in doubly reinforced beam, steel in compression occupies some area of concrete in compression which is needed to be deducted.
modular ratio in compression is 1.5 times the modular ratio in tension i.e. m(compression)=1.5 m(tension), that is why the factor 1.5 for modular ratio
Nice for laborious students of civil engineering