Design of Doubly reinforced beam

Neutral Axis – Solved Example | Doubly reinforced Sections

by

Guide to design of Doubly reinforced Beam

In our article series for “Doubly reinforced sections”, we have covered the following:

What are doubly reinforced sections?

Methods for determining Neutral Axis?

Solved numerical examples for determining Neutral Axis

Numerical examples for practice (Find Neutral axis)

Methods for calculating Moment of Resistance

Numerical example for calculating Moment of resistance

Types of problems in Doubly reinforced sections

Determining stresses in steel and concrete 

Numerical example | Stresses in steel and concrete

Now we shall move on with a solved example. This will help you understand the methods in a better way. I suggest that you do them yourselves too. Practice will help you make your concepts more concrete and clear.

Example:

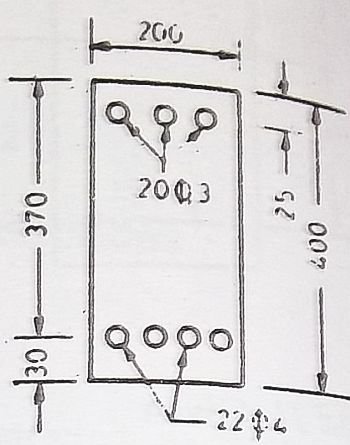
An reinforced concrete beam 200mm x 400mm overall is reinforced with 4 – 22mm⏀ bars with centres 30mm from the bottom edge and 3 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66

Doubly reinforced section diagram
Doubly reinforced section diagram

Given that,

Width of the beam = 200mm

Effective depth of the beam = 400 – 30 = 370mm

Distance of compressive steel from the top edge of the beam to the centre of the steel = d’ = 25mm

Modular ratio = m = 18.66

Area of concrete = Asc = 3 x π/4 x (20)2 = 942 mm2

Area of tensile steel = Ast = 4 x π/4 x (22)2 = 1520 mm2

To find x:

Equating moment of area on compression and tension sides about N.A.

bxx/2 + (1.5m – 1)Asc(x – d’) = mAst (d – x)

200x2/2 + (1.5 x 18.66 – 1) 942 (x – 25)

= 18.66 x 1520 (370 – x)

Therefore, x2 + 537.87x – 111299 = 0

Solving the above equation, we get,

x = 159.579mm

Examples for practice

  • An reinforced concrete beam 300mm x 600mm overall is reinforced with 6 – 22mm⏀ bars with centres 30mm from the bottom edge and 5 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66
  • An reinforced concrete beam 300mm x 600mm overall is reinforced with 4 – 20mm⏀ bars with centres 25mm from the bottom edge and 6 – 20mm⏀ bars with centres 25mm from the top edge. Find the neutral axis of the beam, if m = 18.66